因数定理の威力をさぐる

/剰余定理・因数定理の解説/

17を2,3,5という素数を使って表すと、

この式は次のように解釈できる。

17を3で割ると商が5で余り(剰余)が2となる。

この考え方は $x$ の整式でも適用できる。

例えば $A\left(x\right)$ を $x$ の3次式、 $B\left(x\right)$ を $x$ の2次式とすると

次数でいえばA>B(3次と2次)だから

$A\left(x\right)$ は $B\left(x\right)$ で割ることができる。

そのときの商を $Q\left(x\right)$ 、余りを $R\left(x\right)$ とおくと、

と表すことができる。(①との対応を見て欲しい。)

ここで大事なことは $R\left(x\right)$ の次数は $B\left(x\right)$ が2次式であることから最も高い次数でも1次式となる。
(高々1次式という。)

また、②の両辺は全ての $x$ について成立するので、
$x$ の恒等式である。

今、この関係式を使ってもう少し具体的に整式の割り算について
考えてみる。

$A\left(x\right)$ を実数係数の3次式、 $B\left(x\right)$ を $B\left(x\right)=\left(x-\alpha\right)\left(x-\beta\right)$

商 $Q\left(x\right)$ を $Q\left(x\right)=\left(x-\gamma\right)$ とすると、

余り $R\left(x\right)$ は高々1次式となるから、それを実数p,qを使って表せば、

$R\left(x\right)=px+q$

$\therefore\textcircled{\scriptsize2}$ より

これは $x$ の恒等式であるから、仮に $\left(x-\alpha\right)$ で割るとすると、

その余りは、 $x=\alpha$ を式に代入したときと同じ値になるハズである。

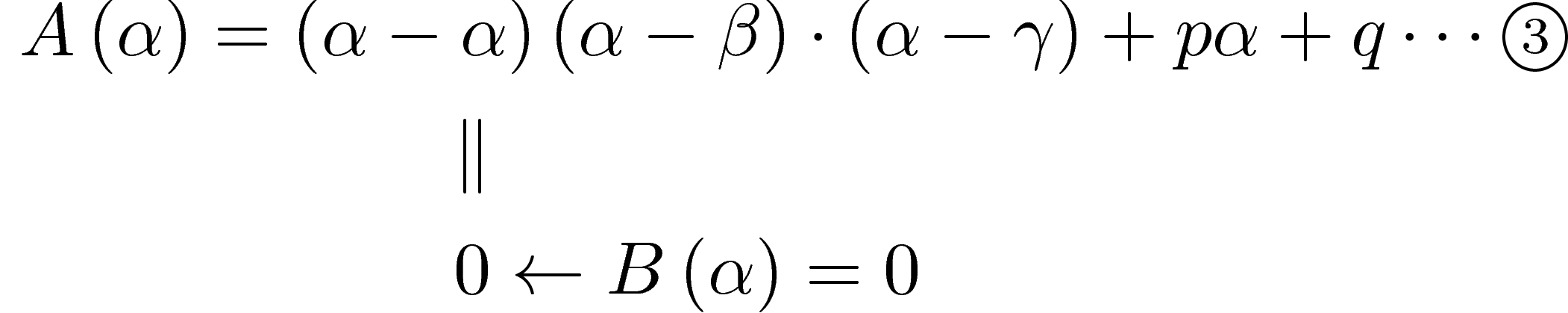
になる。

となって

$\left(x-\alpha\right)$ で割った余りを求めるには $R\left(x\right)$ に

$x=\alpha$ を代入した値と等しくなる。

$\therefore A\left(\alpha\right)=R\left(\alpha\right)$
このことから

「 $x$ の整式 $A\left(x\right)$ を $\left(x-\alpha\right)$ で割ったときの余りは $A\left(\alpha\right)$ で表せる」
これを剰余定理という。

この剰余定理で特に $R\left(\alpha\right)$ が $0$ となるとき、

それは $A\left(x\right)$ が $\left(x-\alpha\right)$ で「割り切れる」ことを意味するから

$\left(x-\alpha\right)$ は $A\left(x\right)$ の因数となる。
(因数分解とは $x$ の多項式を $\left(x-\alpha\right)\left(x-\beta\right)\cdots$ の形で表すことを思い出して欲しい。)

このとき $R\left(\alpha\right)=p\alpha+q=0$ になるから③の例でいえば

ここから
「 $x$ の整式 $A\left(x\right)$ が $\left(x-\alpha\right)$ という因数をもつとき、
その条件は $A\left(\alpha\right)=0$ である」
これを因数定理という。